Publications

Building on recent progress at the intersection of combinatorial optimization and deep learning, we propose an end-to-end trainable architecture for deep graph matching that contains unmodified combinatorial solvers. Using the presence of heavily optimized combinatorial solvers together with some improvements in architecture design, we advance state-of-the-art on deep graph matching benchmarks for keypoint correspondence. In addition, we highlight the conceptual advantages of incorporating solvers into deep learning architectures, such as the possibility of post-processing with a strong multi-graph matching solver or the indifference to changes in the training setting. Finally, we propose two new challenging experimental setups.

Michal Rolínek, Paul Swoboda, Dominik Zietlow, Anselm Paulus, Vít Musil, Georg Martius

ECCV 2020

We present an extension to the disjoint paths problem in which additional lifted edges are introduced to provide path connectivity priors. We call the resulting optimization problem the lifted disjoint paths problem. We show that this problem is NP-hard by reduction from integer multicommodity flow and 3-SAT. To enable practical global optimization, we propose several classes of linear inequalities that produce a high-quality LP-relaxation. Additionally, we propose efficient cutting plane algorithms for separating the proposed linear inequalities. The lifted disjoint path problem is a natural model for multiple object tracking and allows an elegant mathematical formulation for long range temporal interactions. Lifted edges help to prevent id switches and to re-identify persons. Our lifted disjoint paths tracker achieves nearly optimal assignments with respect to input detections. As a consequence, it leads on all three main benchmarks of the MOT challenge, improving significantly over state-of-the-art.

Andrea Hornakova, Roberto Henschel, Bodo Rosenhahn, Paul Swoboda

ICML 2020

We propose a fast approximate solver for the combinatorial problem known as tracking-byassignment, which we apply to cell tracking. The latter plays a key role in discovery in many life sciences, especially in cell and developmental biology. So far, in the most general setting this problem was addressed by off-theshelf solvers like Gurobi, whose run time and memory requirements rapidly grow with the size of the input. In contrast, for our method this growth is nearly linear. Our contribution consists of a new (1) decomposable compact representation of the problem;(2) dual block-coordinate ascent method for optimizing the decompositionbased dual; and (3) primal heuristics that reconstructs a feasible integer solution based on the dual information. Compared to solving the problem with Gurobi, we observe an up to 60 times speed-up, while reducing the memory footprint significantly. We demonstrate the efficacy of our method on real-world tracking problems.

Stefan Haller, Mangal Prakash, Lisa Hutschenreiter, Tobias Pietzsch, Carsten Rother, Florian Jug, Paul Swoboda, Bogdan Savchynskyy

AISTATS 2020

We consider general discrete Markov Random Fields (MRFs) with additional bottleneck potentials which penalize the maximum (instead of the sum) over local potential value taken by the MRF-assignment. Bottleneck potentials or analogous constructions have been considered in (i) combinatorial optimization (e.g. bottleneck shortest path problem, the minimum bottleneck spanning tree problem, bottleneck function minimization in greedoids), (ii) inverse problems with infinity-norm regularization and (iii) valued constraint satisfaction on the (min,max)-pre-semirings. Bottleneck potentials for general discrete MRFs are a natural generalization of the above direction of modeling work to Maximum-A-Posteriori (MAP) inference in MRFs. To this end we propose MRFs whose objective consists of two parts: terms that factorize according to (i) (min,+), i.e. potentials as in plain MRFs, and (ii) (min,max), i.e. bottleneck potentials. To solve the ensuing inference problem, we propose high-quality relaxations and efficient algorithms for solving them. We empirically show efficacy of our approach on large scale seismic horizon tracking problems.

Ahmed Abbas, Paul Swoboda

ICCV 2019

In combinatorial optimization, partial variable assignments are called persistent if they agree with some optimal solution. We propose persistency criteria for the multicut and max-cut problem as well as fast combinatorial routines to verify them. The criteria that we derive are based on mappings that improve feasible multicuts, respectively cuts. Our elementary criteria can be checked enumeratively. The more advanced ones rely on fast algorithms for upper and lower bounds for the respective cut problems and max-flow techniques for auxiliary min-cut problems. Our methods can be used as a preprocessing technique for reducing problem sizes or for computing partial optimality guarantees for solutions output by heuristic solvers. We show the efficacy of our methods on instances of both problems from computer vision, biomedical image analysis and statistical physics.

Jan-Hendrik Lange, Bjoern Andres, Paul Swoboda

CVPR 2019

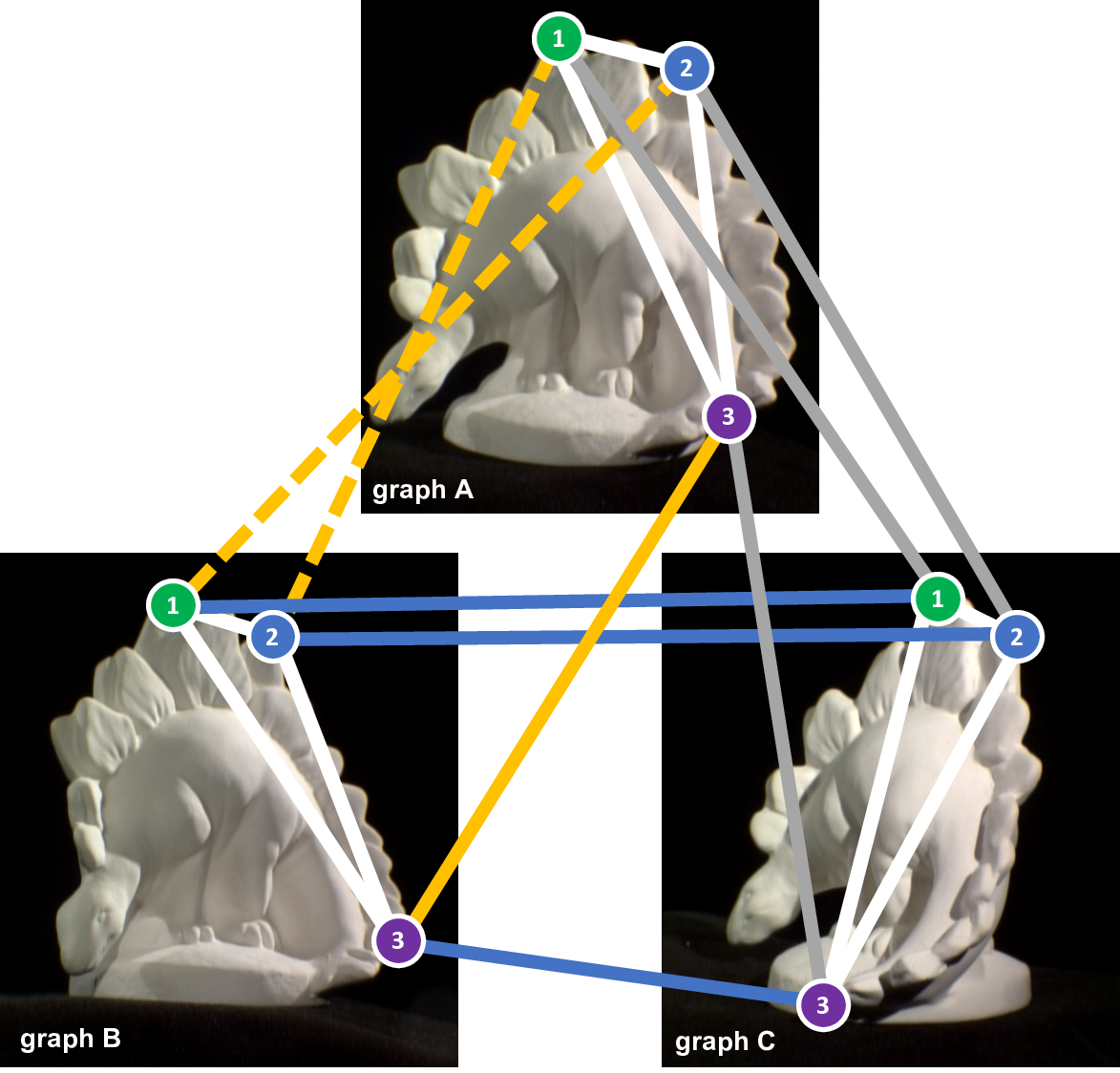
We present a convex relaxation for the multi-graph matching problem. Our formulation allows for partial pairwise matchings, guarantees cycle consistency, and our objective incorporates both linear and quadratic costs. Moreover, we also present an extension to higher-order costs. In order to solve the convex relaxation we employ a message passing algorithm that optimizes the dual problem. We experimentally compare our algorithm on established benchmark problems from computer vision, as well as on large problems from biological image analysis, the size of which exceed previously investigated multi-graph matching instances.

Paul Swoboda, Dagmar Kainmüller, Ashkan Mokarian, Christian Theobalt, Florian Bernard

CVPR 2019

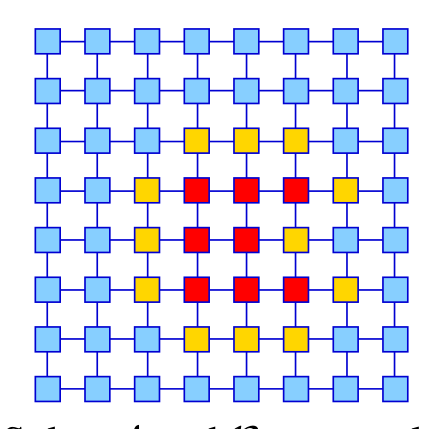
We consider a new relaxation of the MAP-inference problem for MRFs that decomposes the problem into two parts: an easy LP-tight part and a difficult one. These parts are used by efficient message passing and exact ILP solvers respectively, resulting in reduced overall runtime.

Stefan Haller, Paul Swoboda, Bogdan Savchynskyy

AAAI 2018

We introduce a general framework for optimizing Lagrangean decompositions of combinatorial problems based on dual block coordinate ascent.

Paul Swoboda, Jan Kuske and Bogdan Savchynskyy

CVPR 2017

We propose a family of dual block coordinate ascent algorithms for the graph matching problem that surpass state of the art solvers.

Paul Swoboda, Carsten Rother, Hassan Abu Alhaija, Dagmar Kainmüller, Bogdan Savchynskyy

CVPR 2017

We propose a new message passing (a.k.a. dual block coordinate ascent) for the multicut problem (a.k.a. correlation clustering) that outperforms existing LP-based solvers and improves solutions of primal heuristics.

Paul Swoboda, Bjoern Andres

CVPR 2017

We propose a new and tighter relaxation for the multilabel discrete tomography problem and algorithms for solving it.

Jan Kuske, Paul Swoboda, Stefania Petra

SSVM 2017

We propose a new approach to partial optimality that surpasses previous methods both in terms of attained number of persistent variables and runtime.

Alexander Shekhovtsov, Paul Swoboda, Bogdan Savchynskyy

CVPR 2015